|
||||||||||||||||||||||||||||||||||||||||||||||
| Главная страница | Наши разработки | Полезные схемы | Это нужно знать | Вопросы-ответы | Весёлый перекур | ||||||||||||||||||||||||||||||||||||||||||||||
| © 2017 Vpayaem.ru All Rights Reserved |

|

|
Онлайн расчёт активных фильтров на ОУ и транзисторахАктивные ФНЧ, ФВЧ и ПФ второго и третьего порядков А начнём мы с активных фильтров нижних частот (ФНЧ) и фильтров верхних частот (ФВЧ) 2-го и 3-го порядков
имени товарищей Бесселя, Баттерворта и Пафнутия нашего Чебышева. Плавно переходим к активным фильтрам верхних частот (ФВЧ) 2-го и 3-го порядка на ОУ (Рис.2). В транзисторной реализации резисторы, задающие напряжение смещения на базе, уже участвуют в формировании необходимой АЧХ фильтра, поэтому значение Rб1 ll Rб2 должно равняться значению резистора R2 в ФВЧ 2-го порядка, либо R3 в ФВЧ 3-го порядка. 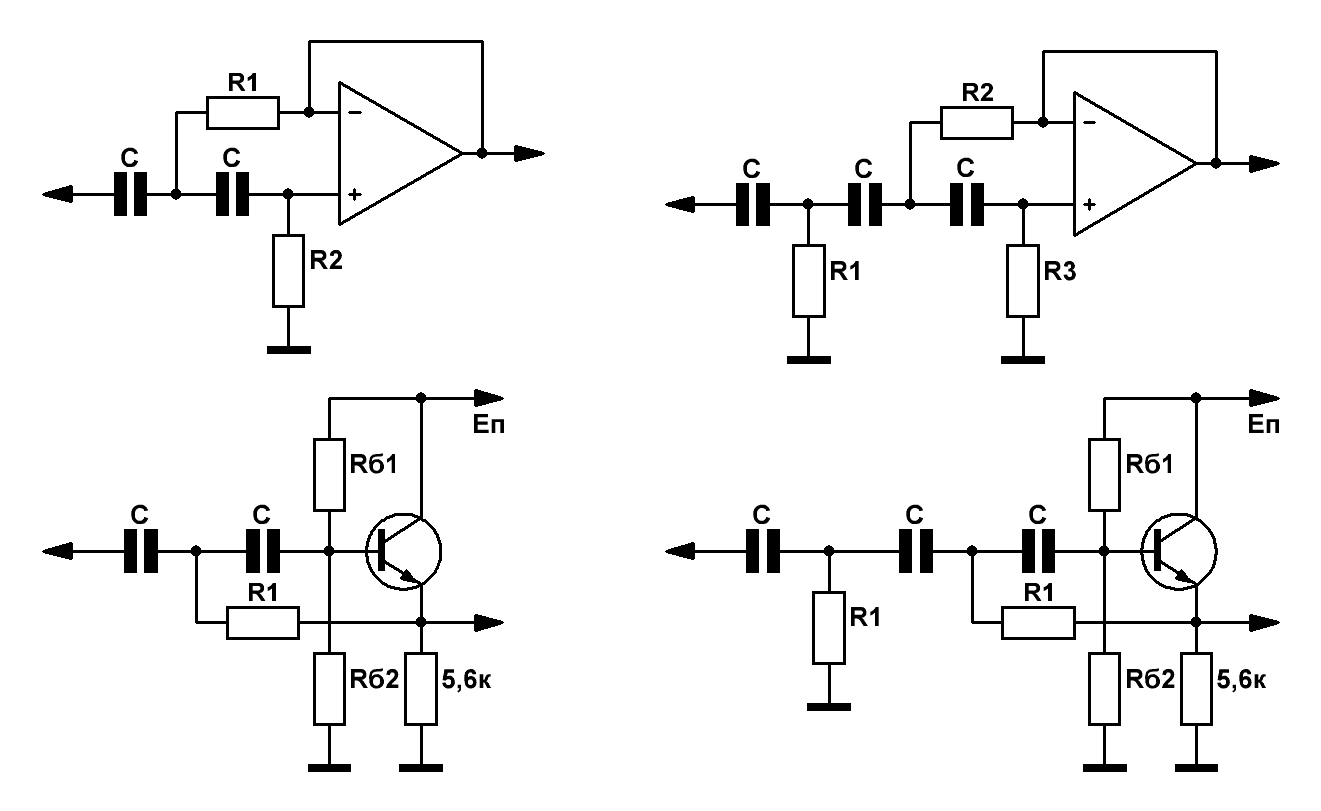 Рис.2 Схемы активных фильтров верхних частот 2-го и 3-го порядков Номиналы элементов рассчитываются исходя из следующих формул: R1=КR1/(2π*F*C) R2=КR2/(2π*F*C) R3=КR3/(2π*F*C) Rrб1llRrб2=R2 для фильтров 2-го порядка, либо Rrб1llRrб2=R3 для 3-го. Для фильтров Баттерворта 2-го порядка КR1=0,707, КR2=1,414, а для фильтров Баттерворта 3-го порядка КR1=0,717, КR2=0,282, КR3=4,950. И опять же, изначально надо определиться с номиналом R1, исходя из принципов, описанных в предыдущих схемах. Онлайн расчёт активных ФВЧ Бесселя, Баттерворта и Чебышева И наконец, мы подобрались к схеме полосового активного фильтра. Здесь всё несколько сложнее, поскольку, при расчёте фильтра, помимо значения центральной частоты, нам не стоит забывать и про такие немаловажные вещи, как коэффициент передачи фильтра в полосе пропускания, да и, собственно, ширину самой полосы пропускания. Формулы, для расчёта элементов: 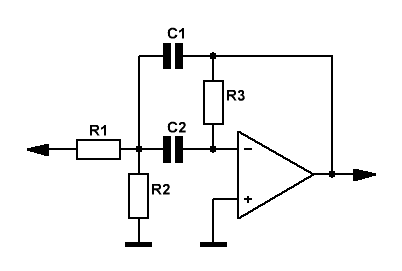 C1=C2=C
C1=C2=C R1=Q/(2πF*Kп*C) R2=Q/((2πF*C*(2Q²-Kп)) R3=2Q/(2πF*C) Q=F/Bпр, где: Q-добротность фильтра, Впр-полоса пропускания по уровню -3дБ, F-центральная частота фильтра, Кп-коэффициент передачи фильтра в полосе пропускания. Рис.3 Схема активного полосового фильтра 2-го порядка В фильтре, приведённом на рисунке, не стоит слишком усердствовать с высокими значениями добротности и коэффициента передачи. Как показывает практика, и тот и другой параметр следует ограничить сверху на уровне 5...6 единиц. Как всегда, начинаем с выбора номинала резистора R1, который как минимум в 10 раз должен быть выше выходного импеданса предыдущего каскада. Калькулятор расчёта активного полосового фильтра 2-го порядка
ВНИМАНИЕ!!! Для правильной работы этого фильтра должно соблюдаться условие К<2*Q². При несоблюдении этого условия, значение R2 в таблице примет отрицательное значение. А что делать, если полученные значения элементов не попадают в стандартную сетку? Не беда, нарисуем ещё одну таблицу, но до этого надо поиграться коэффициентом передачи фильтра в небольших пределах (например, сделать не 1,5, а 1,45, или 1,55) до достижения значения R3 величины, попадающей в сетку. Номинал R1 мы уже выбрали, исходя из соображений приемлемого входного импеданса. Предположим, нам надо рассчитать фильтры для 10-полосного эквалайзера. Фильтры у нас получаются октавные, стандартное значение добротности для них Q=1,41. R1 выберем номиналом 30кОм, Кпер = 1,5. Произведём расчёт для частоты 1000 Гц. Подставив эти цифры в верхнюю таблицу, получаем С=4987пФ, R2=18,173кОм, R3=90кОм. Пошебуршав туда-сюда Кпер, понимаем, что для получения стандартного значения R3=91кОм, коэффициент передачи фильтра должен быть равен 1,517, что для нашего случая вообще не принципиально, тем более, что это значение Кпер будет сопровождать все фильтры, независимо от частоты. Итак, подставляем в нижнюю таблицу R1=30кОм, R3=91кОм, R2=18кОм, стандартное значение ёмкости С=5100пФ и естественным образом видим, что значение резонансной частоты у нас съехало до 975Гц. Но у нас было с собой, а именно замечательное сопротивление R2, которое никак не влияет на Кпер, и весьма скромно - на добротность. Покрутив номинал этого резистора, получаем - 16,7кОм, центральную частоту - 999Гц и добротность - 1.46. Всё, расчёт фильтра - завершён. Ещё один калькулятор для активного полосового фильтра
Для желающих рассчитать параметры и элементы многополосных графических эквалайзеров следует посетить страницу ссылка на страницу , а на следующей странице мы рассмотрим универсальный перестраиваемый активный фильтр с регулировкой частоты и добротности.
|