Скин-эффект в проводнике
Что такое скин-эффект и как он влияет на сопротивление провода? Онлайн калькуляторы расчёта глубины скин-эффекта, а также сопротивления проводника с учётом поверхностного эффекта
Довольно часто при изготовлении высокодобротной катушки индуктивности либо мощного импульсного трансформатора разработчик сталкивается с тем, что
практические результаты существенно не совпадают с проведёнными расчётами.
Давайте разберёмся – а из-за чего, собственно говоря, такое может происходить?
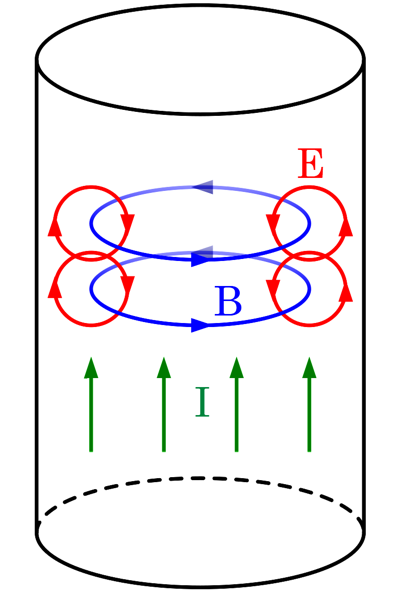
При протекании переменного тока по проводнику вокруг него и внутри образуется магнитный поток (В), силовые линии которого перпендикулярны оси проводника.
Рис.1 Скин-эффект в проводнике
За счёт электромагнитной индукции переменное магнитное поле порождает вихревое электрическое поле (Е), причём на поверхности проводника вектор напряжённости
электрического поля направлен по направлению тока проводника, а внутри проводника – противоположно (Рис.1).
Именно это явление и получило название поверхностного эффекта или скин-эффекта. Приведём формулировку:
Скин-эффект или поверхностный эффект – это эффект уменьшения амплитуды электромагнитных волн, а соответственно, и тока в зависимости от
степени их проникновения внутрь среды проводника. А это означает то, что переменный электрический ток циркулирует по большей части в области поверхности провода,
причём глубина его проникновения внутрь проводника тем больше, чем ниже частота протекающего тока. При постоянном протекающем токе скин-эффект сходит на нет
и никак себя не проявляет.
Рассмотрим это явление в виде поясняющих картинок:
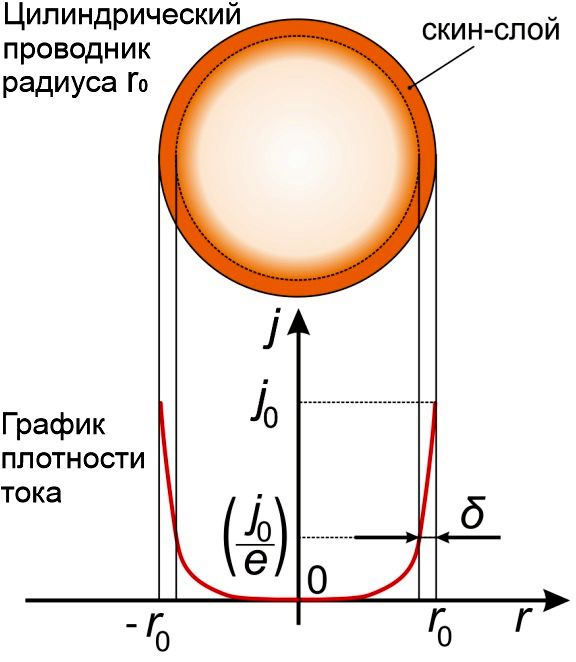
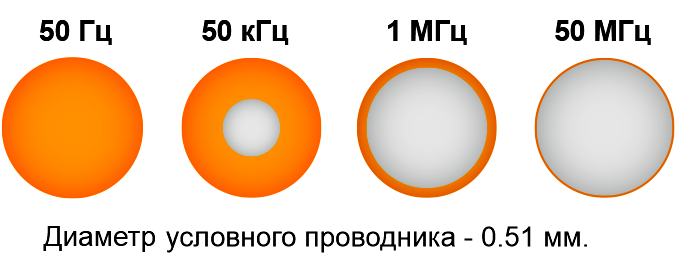 Рис.2 Распределение плотности тока в цилиндрическом проводнике и
Рис.2 Распределение плотности тока в цилиндрическом проводнике и
зависимость глубины проникновения от частоты
Распределение тока внутри проводника имеет экспоненциальный характер, поэтому в первом приближении можно считать, что электрический
ток имеет относительно равномерную зависимость только в поверхностном слое, называемым скин-слоем, а в остальном сечении
настолько мал, что им можно пренебречь.
Толщина скин-слоя (обозначается δ или Δ) – это глубина, на которой плотность тока внутри проводника уменьшается в е = 2,71828 раз
(до 37% от поверхностной).
Численно эта величина равна:
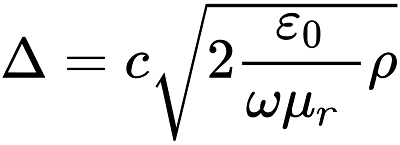 , где , где
с – это скорость света: 299 792 458 м/с,
ε0 – электрическая постоянная 8,85419⋅10−12 Ф/м,
ρ – удельное сопротивление проводника,
ω = 2πf – круговая (циклическая) частота,
μr – относительная магнитная проницаемость, которая для
всех диамагнетиков и парамагнетиков, таких как: алюминий, медь, олово, свинец, цинк, серебро, золото и т. д., с точностью до трёх знаков
после запятой равна 1.
Для проверки формул приведём онлайн калькулятор по расчёту толщины скин-слоя, но для начала:
Таблица значений удельного сопротивления некоторых металлов
| Металл |
Удельное сопротивл. Ом*мм2/м |
Металл |
Удельное сопротивл. Ом*мм2/м |
Металл |
Удельное сопротивл. Ом*мм2/м |
| Медь |
0,0172...0,018 |
Серебро |
0,015...0,0162 |
Нихром |
1,05...1,4 |
| Алюминий |
0,026...0,0295 |
Платина |
0,107 |
Латунь |
0,025...0,108 |
| Сталь |
0,103...0,137 |
Цинк |
0,059 |
Бронза |
0,095...0,1 |
| Олово |
0,12 |
Железо |
0,098 |
Золото |
0,023 |
| Свинец |
0,217...0,227 |
Никель |
0,087 |
Вольфрам |
0,053...0,055 |
А теперь:
Онлайн расчёт толщины скин-слоя
Определение изменённого (по сравнению с постоянным током) значения сопротивления проводника, работающего в условиях протекания по нему переменного тока, дело
куда более сложное, чем расчёт толщины скин-слоя. Большинство отечественных источников отсылает нас к функциям Бесселя и уравнениям Максвелла.
Однако, как и во многих других случаях, на помощь приходят зарубежные источники, которые приводят простой и наглядный график отношения сопротивления переменному
току к сопротивлению постоянному току в зависимости от отношения радиуса круглого провода к глубине скин-слоя:
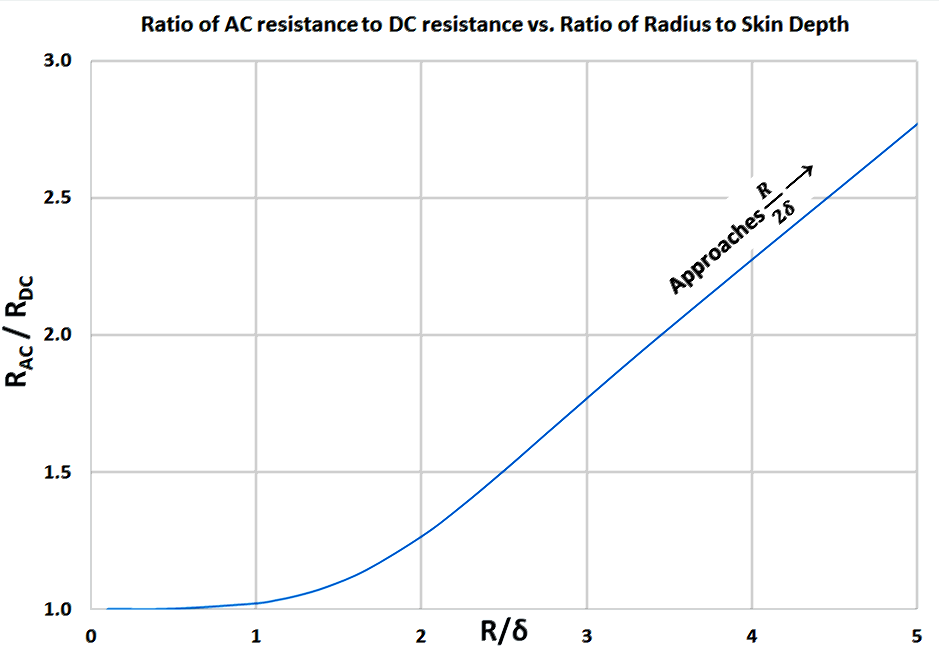
Рис.3 Зависимость отношения сопротивления круглого проводника переменному току к сопротивлению постоянному току в зависимости от отношения радиуса
к глубине скин-слоя
Если задаться сопротивлением проводника постоянному току, которое можно легко рассчитать по формуле
R = ρ*l/S
или на калькуляторе на странице [ссылка на страницу], а также глубиной скин-эффекта, то приведённый график
позволит без всяких уравнений Бесселя и Максвелла найти искомое сопротивление переменному току.
Методом аппроксимации данный график можно описать функциями и для удобства дополнить его онлайн калькулятором.
Онлайн расчёт отношения сопротивлений провода постоянному и переменному току
|


