Электрический ток. Закон Ома для участка цепи и полной цепи постоянного и переменного токов

Онлайн расчёт электрических величин напряжения, тока и мощности с резистивными, ёмкостными и индуктивными элементами. Закон Ома простыми словами, теория и практика для начинающих

Начнём с терминологии.
Электрический ток – это направленное движение заряженных частиц, при котором происходит перенос заряда из одной области электрической цепи в другую.
Силой электрического тока (I) является величина, которая численно равна количеству заряда Δq, протекающего через заданное поперечное сечение проводника S за единицу времени Δt: I = Δq/Δt.
Напряжение электрического тока между точками A и B электрической цепи - физическая величина, значение которой равно работе эффективного электрического поля, совершаемой при переносе единичного пробного заряда из точки A в точку B.
Омическое (активное) сопротивление – это сопротивление цепи постоянному току, вызывающее безвозвратные потери энергии постоянного тока.
Теперь можно переходить к закону Ома.

Закон Ома был установлен экспериментальным путём в 1826 году немецким физиком Георгом Омом и назван в его честь. По большому счёту, Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, определяющих зависимость между электрическими величинами, такими как: напряжение, сопротивление и сила тока исключительно для проводников, обладающих постоянным сопротивлением. При расчёте напряжений и токов в нелинейных цепях, к примеру, таких, которые содержат полупроводниковые или электровакуумные приборы, этот закон в простейшем виде уже использоваться не может.

Тем не менее, закон Ома был и остаётся основным законом электротехники, устанавливающим прямую связь силы электрического тока с сопротивлением и напряжением, и является самым востребованным как для начинающего радиолюбителя, так идля профессионального разработчика.

Формулировка закона Ома для участка цепи может звучать так: Сила тока в проводнике прямо пропорциональна напряжению (разности потенциалов) на его концах и обратно пропорциональна сопротивлению этого проводника и записана в следующем виде: I=U/R,

где: I – сила тока в проводнике, измеряемая в амперах [А];
U – напряжение (разность потенциалов) в вольтах [В];
R – электрическое сопротивление проводника в омах [Ом].


Производные от этой формулы приобретают такой же незамысловатый вид:
R=U/I и U=R×I.

Зная любые 2 из 3-ёх приведённых параметров, можно произвести также расчёт величины мощности, рассеиваемой на сопротивлении нагрузки.

Мощность является функцией протекающего черех нагрузку тока I(А) и приложенного напряжения U(В) и вычисляется по следующим формулам, также являющимся производными от основной формулы закона Ома:
P_(Вт) = U_(В)×I_(А) = I²_(А)×R_(Ом) = U²_(В)/R_(Ом)

Формулы, описывающие закон Ома, настолько просты, что не стоят выеденного яйца и, возможно, вообще не заслуживают отдельной крупной статьи на страницах уважающего себя сайта.
Не заслуживают, так не заслуживают. Деревянные счёты Вам в помощь, уважаемые дамы и рыцари! Считайте, однако учитывайте размерность, не стирайте из памяти:

Единицы измерения напряжения: 1 В = 1000 мВ = 1000000 мкВ;
Единицы измерения силы тока: 1 А = 1000 мА = 1000000 мкА;
Единицы измерения сопротивления: 1 Ом = 0.001 кОм = 0.000001 МОм;
Единицы измерения мощности: 1 Вт = 1000 мВт = 100000 мкВт.

Ну и так, на всякий случай, чисто для проверки полученных результатов, приведём незамысловатый калькулятор, позволяющий в онлайн режиме проверить расчёты, связанные со знанием формул закона Ома.

Калькулятор для проверки результатов расчёта закона Ома

Вводить в калькулятор нужно только два имеющихся у Вас параметра, остальные посчитаются сами.

Напряжение U		В мВ мкВ
Сопротивление R		Ом кОм МОм
Сила тока I		А мА мкА
Мощность Р		Вт мВт мкВт

Все наши расчёты проводились при условии, что значение внешнего сопротивления R значительно превышает внутреннее сопротивление источника напряжения r_внутр.
Если это условие не соблюдается, то под величиной R следует принять сумму внешнего и внутреннего сопротивлений: R = R_внешн + r_внутр.
После этого закон приобретает более солидное название – закон Ома для полной цепи, а формула становится: I=U/(R+r) .

Для многозвенной цепи необходимо преобразовать её к эквивалентному виду: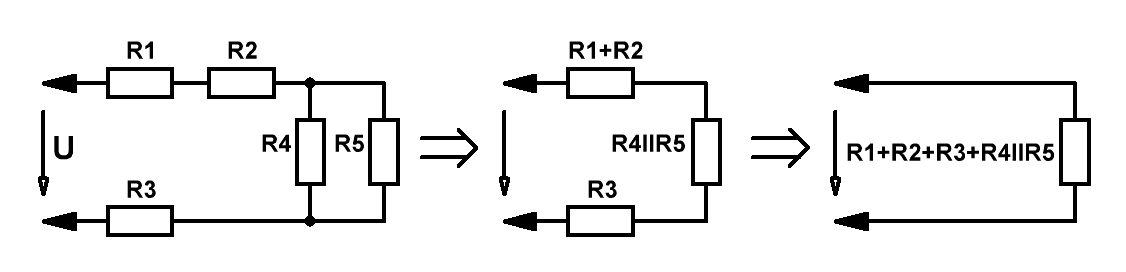


Значения последовательно соединённых резисторов просто суммируются, в то время как значения параллельно соединённых резисторов определяются исходя из формулы: 1/R_ll = 1/R₄+1/R₅.
Онлайн калькулятор для расчёта величин сопротивлений при параллельном соединении нескольких резисторов можно найти на странице ссылка на страницу.

Теперь, что касается закона Ома для переменного тока.
Если внешнее сопротивление у нас чисто активное (не содержит ёмкостей и индуктивностей), то формула, приведённая выше, остаётся в силе.
Единственное, что надо иметь в виду для правильной интерпретации закона Ома для переменного тока – под значением U следует понимать действующее (эффективное) значение амплитуды переменного сигнала.

А что такое действующее (эффективное) значение и как оно связано с амплитудой сигнала переменного тока?
Приведём диаграммы для нескольких различных форм сигнала.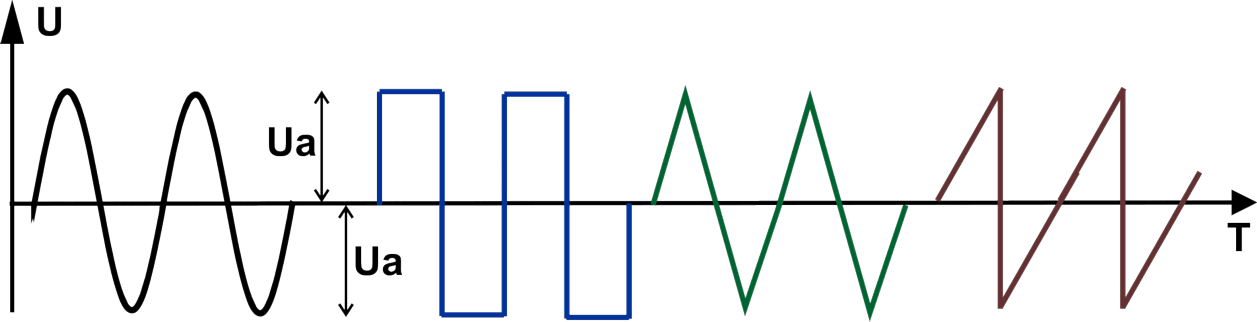



Слева направо нарисованы диаграммы синусоидального сигнала, меандра (прямоугольный сигнал со скважностью, равной 2), сигнала треугольной формы, сигнала пилообразной формы.
Глядя на рисунок можно осмыслить, что амплитудное значение приведённых сигналов – это максимальное значение, которого достигает амплитуда в пределах положительной, или отрицательной (в наших случаях они равны) полуволны.

Рассчитать действующее значение напряжение интересующей нас формы можно по следующим соотношениям:
1. Для синуса – U = Uд = Uа/√2;
2. для треугольника и пилы – U = Uд = Uа/√3;
3. для меандра – U = Uд = Uа.

С этим разобрались!
А теперь посмотрим, как будет выглядеть формула закона Ома при наличии индуктивности или ёмкости в цепи переменного тока.
В общем случае выглядеть это будет так: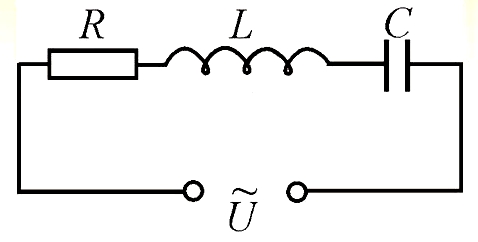



А формула остаётся прежней, просто в качестве сопротивления R выступает полное сопротивление цепи Z, состоящее из активного, ёмкостного и индуктивного сопротивлений.
Поскольку фазы протекающего через эти элементы тока не одинаковы, то простым арифметическим сложением сопротивлений этих трёх элементов обойтись не удаётся, и формула приобретает вид: .

Реактивные сопротивления конденсаторов и индуктивностей мы с Вами уже рассчитывали на странице – (ссылка на страницу) и знаем, что величины эти зависят от частоты, протекающего через них тока и описываются формулами:
X_C = 1/(2πƒС) ,   X_L = 2πƒL .

Нарисуем ещё один калькулятор для расчёта полного сопротивления цепи для переменного тока.
Количество вводимых элементов должно быть не менее одного, при наличии индуктивного или емкостного элемента – необходимо указать значение частоты f.

Онлайн расчёт полного сопротивления цепи

Сопротивление R		Ом кОм МОм
Индуктивность L		Гн мГн мкГн
Ёмкость С		МкФ  нФ пФ
Частота f		Гц кГц МГц
Реактивное сопротивление XC
Реактивное сопротивление XL
Полное сопротивление цепи Z

А теперь рассмотрим практический пример применения закона Ома для цепей переменного тока и рассчитаем простой бестрансформаторный источник питания.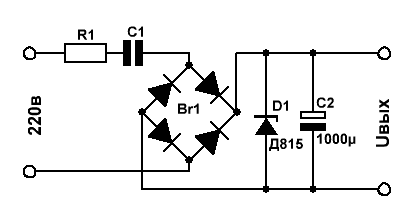

Токозадающими цепями в данной схеме являются элементы R1 и С1.
Допустим, нас интересует выходное напряжение Uвых = 12 вольт при токе нагрузки 100 мА.
Выбираем стабилитрон Д815Д с напряжением стабилизации 12В и максимально допустимым током стабилизации 1,4А.
Зададимся током через стабилитрон с некоторым запасом – 200мА.
С учётом падения напряжения на стабилитроне, напряжение на токозадающей цепи равно 220в – 12в = 208в.
Теперь рассчитаем сопротивление этой цепи Z для получения тока, равного 200мА:
Z = 208в/200мА = 1,04кОм.
Резистор R1 является токоограничивающим и выбирается в пределах 10...100 Ом в зависимости от максимального тока нагрузки.
Зададимся номиналами R1 = 30 Ом, С1 = 1 Мкф, частотой сети f = 50 Гц и подставим всё это хозяйство в калькулятор.
Получили полное сопротивление цепи, равное 3.183кОм. Многовато будет – надо увеличивать ёмкость С1.
Поигрались туда-сюда, нашли нужное значение ёмкости – 3,18 Мкф, при котором Z = 1,04кОм.
Всё – закон Ома выполнил свою функцию, расчёт закончен.