Параллельный и последовательный колебательный контур

Что такое колебательный LC-контур? Принцип работы, формулы расчёта основных параметров. Онлайн калькулятор резонансной частоты колебательного контура, добротности и коэффициента затухания в зависимости от величин индуктивности, ёмкости и сопротивления потерь

Колебательный контур – это пассивная электрическая цепь, которая состоит из конденсатора и катушки индуктивности, в которой возможно возбудить свободные электромагнитные колебания.
Если конденсатор и катушка соединены параллельно, то контур называется параллельным, при последовательном соединении элементов колебательный контур называется последовательным.

Для начала давайте рассмотрим параллельный колебательный контур, который в радиотехнике используется как основа частотно-избирательных цепей и встречается намного чаще последовательного.

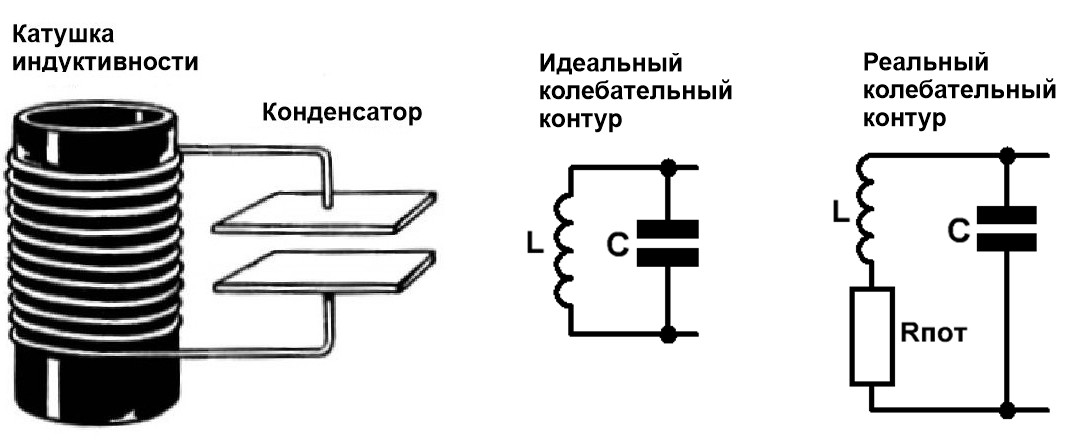
Рис.1 Параллельный колебательный контур, его изображение на схеме
(идеальный колебательный контур), реальный колебательный контур

При анализе цепи колебательного контура обычно используется реалистичная модель (Рис.1 справа), состоящая из идеальных пассивных элементов и активного сопротивления потерь катушки – Rпот. Сопротивление потерь катушки Rпот складывается из потерь в проводах, диэлектрике, сердечнике и экране (если он есть).
Поскольку потери в контурном конденсаторе на порядки меньше, чем потери в катушке, то его сопротивление потерь при расчётах обычно не учитывается.

Так, за счёт чего в колебательном контуре возникают свободные колебания? Для того чтобы ответить на этот вопрос, давайте соберём простейшую схему (Рис.2)


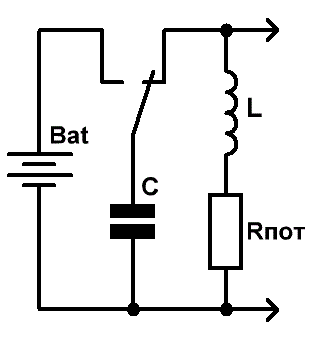
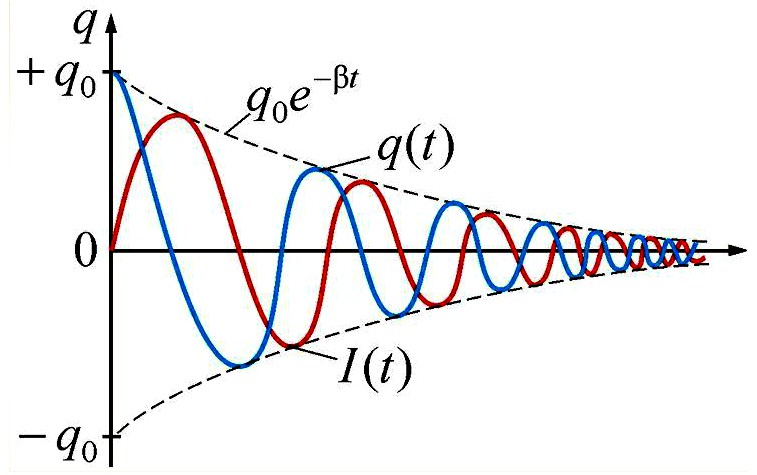
Рис.2 Колебательный процесс в параллельном колебательном контуре

Для возбуждения в контуре колебаний конденсатор следует предварительно зарядить, сообщая его обкладкам заряд q_max от внешнего источника Bat напряже- нием U_max. После того как конденсатор будет заряжен, переводим переключатель в правое по схеме положение, отключая контур от источника, и наблюдаем возникшие в цепи затухающие электромагнитные колебания, при которых происходит превращение энергии электрического поля в энергию магнитного поля и наоборот (Рис.2 справа).

Из-за потерь, возникающих в элементах контура, электромагнитные колебания в цепи всегда будут затухающими. Скорость их затухания зависит от величины этих потерь, суммарное значение которых характеризуются параметром, называемым добротностью колебательного контура Q. Численно добротность равна числу колебаний от момента возбуждения свободных колебаний до момента, когда их амплитуда уменьшится в еπ = 23,14 раз. Для желающих поподробнее познакомиться с тем, что такое добротность и как её измерить, имеет смысл посетить страницу – ссылка на страницу.
А мы тем временем рассмотрим последовательные фазы колебаний, происходящие в контуре после зарядки конденсатора.



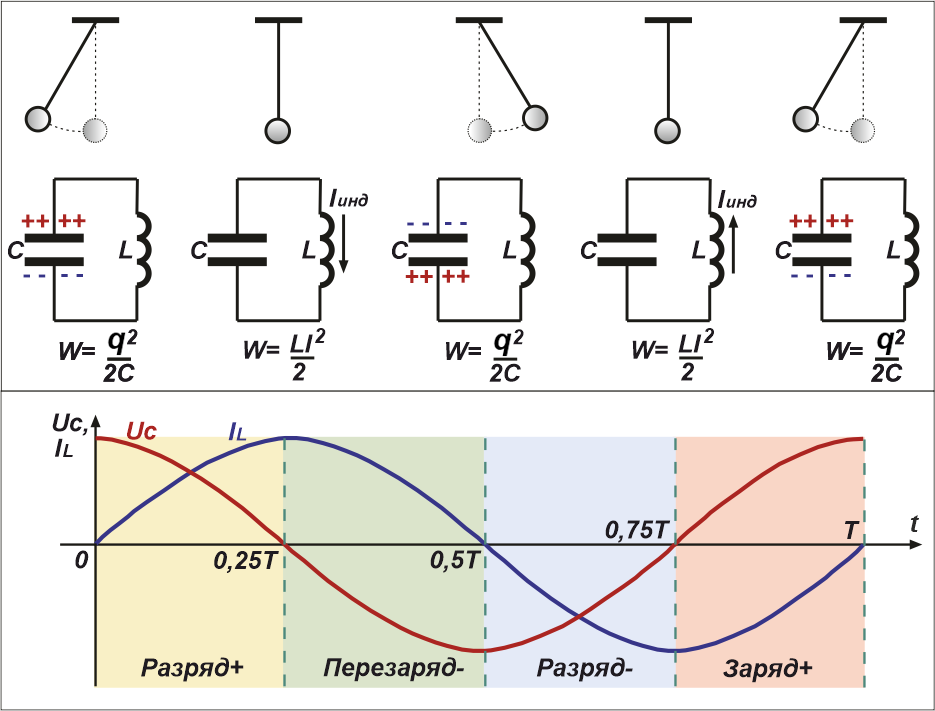
Рис.3 Фазы колебаний в колебательном контуре за полный период

Электромагнитные колебания, а также описывающие их уравнения во многом подобны механическим колебаниям.

Опишем стадии колебательного процесса за полный период колебаний:
1. t = 0 – начало разрядки конденсатора (энергия электрического поля, запасённая в конденсаторе, равна W = q²/2C ). Через катушку начинает течь ток. При этом катушка оказывает сопротивление моментальному росту тока, поскольку в ней присутствует ЭДС самоиндукции, препятствующая этому росту.
2. t = 0.25Т – конденсатор полностью разряжен. Ток через катушку максимален, так как вся энергия из конденсатора перешла в энергию магнитного электрического поля катушки W = L*I²/2. Начиная с этого момента, эта энергия начинает опять перетекать в конденсатор, перезаряжая его потенциалом обратной полярности.
3. t = 0.5Т – конденсатор опять полностью заряжен, но потенциалом противоположной полярности. Ток через катушку индуктивности равен нулю. Начинается фаза, описанная в п.1, но с током, текущем в обратном направлении.
4. t = 0.75Т – конденсатор вновь полностью разряжен, ток через катушку максимален и направлен в противоположную (по отношению к п.2) сторону.
5. t = Т – всё начинается сначала, т. е. аналогично 1п.

А теперь: Формулы для расчёта колебательного LC контура:

Период колебаний: T₀ = 2π√LC ;
Частота: F₀ = 1/T₀ ;
Круговая (циклическая) частота: ω₀ = 2π/T₀ = 2πF₀ ;
Максимальный заряд конденсатора: q_max = U_maxC ;
Максимальная сила тока через катушку: I_max = ωq_max .
Добротность колебательного контура: ;

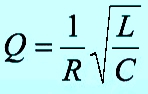Мгновенные значения напряжения, тока и энергии рассчитываются по формулам:
Заряд: q(t) = q_max cos(ωt) ;
Напряжение: U(t) = U_max cos(ωt) ;
Сила тока: I(t) = I_max sin(ωt) ;
Энергия: W(t) = I(t)²L/2 + q(t)²/(2C) .

Все приведённые формулы хороши для идеального колебательного контура, в котором нет потерь, а соответственно, и нет затухания колебаний. Для реальных же контуров (с потерями) вводятся дополнительные параметры, характеризующие скорость затухания колебаний. Одними из таких параметров являются коэффициент затухания β и логарифмический декремент колебаний λ.
Коэффициент затухания β – это величина, характеризующая скорость затухания колебаний и обратно пропорциональная времени τ, по истечении которого амплитуда колебаний убывает в е раз. Для колебательного контура данная величина вычисляется по формуле: β = R_потерь /(2L).
Логарифмическим декрементом затухания λ называется величина, равная натуральному логарифму отношения двух последовательных амплитуд, отстоящих друг от друга на период колебаний. Численно логарифмический декремент равен коэффициенту затухания, умноженному на период колебаний: λ = βT.

С учётом коэффициента затухания формулы приобретают следующий вид:

Заряд: q(t) = q_max cos(ωt) e^(-βt) ;
Напряжение: U(t) = U_max cos(ωt) e^(-βt) ;
Сила тока: I(t) = I_max sin(ωt) e^(-βt) ;
Энергия: W(t) = I(t)²L/2 + q(t)²/(2C) ;
Период: ;
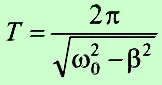Круговая (циклическая) частота: ;

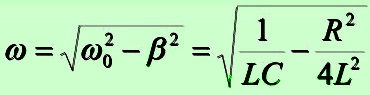Добротность: Q = Lω/R .

При относительно высокой добротности цепи, то есть когда колебания затухают не слишком быстро и выполняется условие β² << ω₀², круговая частота контура равна ω ≈ ω₀ , а формулы по расчёту резонансной частоты и добротности принимают привычный вид, приведённый выше на синем фоне.

Для проверки знаний, полученных в рамках данной статьи, приведём онлайн калькулятор для расчёта основных параметров колебательного контура.

Расчёт резонансной частоты, добротности и коэффициента
затухания контура

Ёмкость конденсатора контура		пФ нФ МкФ
Индуктивность катушки контура L		мкГн мГн Гн
Сопротивление потерь Rпот		Ом кОм
Резонансная частота
Добротность = кол-во колебаний
Коэффициент затухания β (сек-1)

Для последовательного колебательного контура резонансная частота (период и круговая частота) не зависит от сопротивления потерь, однако остальные приведённые выше параметры описываются теми же формулами, что и для параллельного. При этом в составе частотно-избирательных цепей эти контуры ведут себя по-разному и имеют значительно отличающиеся друг от друга передаточные характеристики. Какие это характеристики? – рассмотрим в рамках отдельной статьи.

А на следующей странице рассмотрим, как на добротность LC-контура влияют сопротивления нагрузки и источника сигнала.

Дальше