Онлайн расчёт LC фильтров 2-го порядка

Калькуляторы ФНЧ, ФВЧ, резонансных, полосовых LC - фильтров

LC - фильтры я оставил на десерт подобно бутылке благородного вина, покрытой слоем вековой пыли. Этот антиквариат является наиболее древним из семейства фильтров второго и более высоких порядков и если в области низких частот в настоящее время в основном применяются активные RC-фильтры, то в радиочастотной схемотехнике LC-цепи до сих пор находят своё главенствующее применение.

На Рис.1 изображён параллельный LC колебательный контур.
Частотная зависимость коэффициента передачи такого LC контура соответствует характеристике резонансного полосового фильтра. Именно с этого самого простого LC-фильтра мы и начнём расчёт.

Как уже было сказано, приведённый LC контур – это узкополосный полосовой резонансный фильтр, настроенный на частоту: fо= 1/(2π√LС).

На резонансной частоте сопротивление контура равно: Rо = ρQ, где ρ – это характеристическое сопротивление контура, численно равное: ρ = √L/C, а
Q = fо/Δf - это параметр добротности LC контура, определяющий полосу пропускания фильтра по уровню 3 дБ.

Рис.1 Параллельный LC колебательный контур

Рассчитать добротность контура можно по формуле Q= ρ/R_пот= (√L/C)/R_пот , где R_пот – это сумма сопротивлений потерь: в катушке индуктивности L1 (обусловленных активным сопротивлением катушки, потерями в каркасе, экране, сердечнике и т.д) и в конденсаторе C1 (обусловленных потерями в диэлектрике).

На низких частотах конденсатор практически не вносит потерь, поэтому добротность контура равна добротности катушки индуктивности, величина которой в основном зависит от активного сопротивления катушки. Чем ниже частота, тем больше витков и тоньше провод, тем проще измерить его активное сопротивление тестером и учесть это значение в расчётах.
На радиочастотах значение активного сопротивления катушки может составлять омы или доли ома. Однако при расчёте сопротивления потерь приходится учитывать и другие факторы, в результате которых общее сопротивление может в разы превышать активное.

Переходим к калькулятору по расчёту параметров LC узкополосного полосового (резонансного) фильтра, построенного по схеме параллельного резонансного контура.
Необходимо отметить, что полученные в калькуляторе данные верны и для последовательного колебательного контура. При этом если мы хотим использовать свойства контура полностью, то есть получить острую резонансную кривую, соответствующую конструктивной добротности катушки, то параллельный контур надо нагружать слабо, выбирая R1 и Rн намного больше Rо (на практике десятки-сотни кОм), для последовательного же контура, сопротивление генератора R1 наоборот должно быть на порядки меньше характеристического сопротивления ρ.

Онлайн расчёт резонансной частоты, добротности и полосы
пропускания LC - резонансного (полосового) фильтра

Ёмкость конденсатора контура		пФ нФ МкФ
Индуктивность катушки контура L		мкГн мГн Гн
Сопротивление потерь Rпот		Ом кОм
Резонансная частота
Добротность фильтра Q
Характеристическое сопротивление ρ (Ом)
Сопротивление контура на рез. частоте (Ом)
Полоса пропускания фильтра

Теперь плавно переходим к LC фильтрам верхних и нижних частот (ФВЧ и ФНЧ).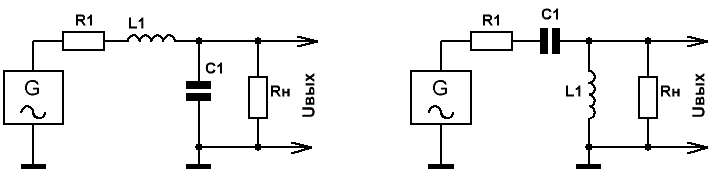

Рис.2 LC фильтры верхних и нижних частот 2-го порядка

В полосе пропускания коэффициент передачи по напряжению данных фильтров близок к единице при условии R1 << ρ << Rн, где R1 - внутреннее сопротивление генератора, Rн - сопротивление нагрузки, а ρ - характеристическое сопротивление фильтра.
Однако оптимальные параметры, с точки зрения равномерности АЧХ и передачи максимальной мощности в нагрузку, обеспечиваются при R1 = Rн = ρ. В этом случае фильтр является согласованным, правда коэффициент передачи в полосе пропускания становится равным К=0.5.

Номиналы элементов и параметры ФВЧ и ФНЧ вычислим для согласованных LC фильтров. За частоту среза, как водится, примем частоту, на которой ослабление сигнала составляет 3дБ. Крутизна спада АЧХ в полосе подавления таких фильтров составляет 12 дБ/октаву.
Ну да ладно, ближе к делу.

Онлайн расчёт LC-фильтров верхних и нижних частот

Характеристика фильтра	ФНЧ ФВЧ
Индуктивность катушки L1		Миллигенри  Микрогенри
Ёмкость конденсатора С1		Микрофарад Нанофарад Пикофарад
Частота среза фильтра Fср.
Характеристическое сопротивление ρ (Ом)

А если надо рассчитать L и C при известных значениях Fср и ρ?

Ещё один расчёт LC-фильтров верхних и нижних частот

Характеристика фильтра	ФНЧ ФВЧ
Частота среза фильтра Fср.		Герц Килогерц Мегагерц
Характеристическое сопротивление ρ (Ом)
Индуктивность катушки L1
Ёмкость конденсатора С1

В последнее время мне на почту приходит всё большее количество вопросов по поводу LC-фильтров для акустических систем, то есть фильтров, для которых входным источником является усилитель с практически нулевым внутренним сопротивлением, а нагрузкой - динамическая головка, обладающая неким (условно примем) активным импедансом.
Естественно, что расчёт элементов, выполненный с помощью приведённых выше калькуляторов для согласованных цепей, ожидаемых результатов не даст ни с точки зрения частоты среза фильтра, ни с точки зрения - равномерности его АЧХ. Поэтому вдогонку размещу-ка я и калькулятор для расчёта НЧ-ВЧ фильтров для акустики, либо каких иных приложений, где величина сопротивления источника имеет величину значительно меньшую, чем Rн.
Плюсом этих фильтров является близкий к единице коэффициент передачи сигнала, минусом - меньшая (чем у согласованных) крутизна спада АЧХ в полосе подавления, которая составляет 10 против 12 дБ/октаву.

Расчёт LC-фильтров ФВЧ и ФНЧ для акустики и прочего

Характеристика фильтра	ФНЧ ФВЧ
Частота среза фильтра Fср.		Герц Килогерц Мегагерц
Сопротивление нагрузки Rн (Ом)
Индуктивность катушки L1
Ёмкость конденсатора С1

Фильтры, рассчитанные на этом калькуляторе, являются фильтрами Баттерворта 2-го порядка. А желающим получить разнообразные и полноценные акустические ФВЧ, ФНЧ и ПФ различных типов и порядков рекомендую посетить страницу: ссылка на страницу.

Приведённые выше ФВЧ и ФНЧ называются Г-образными.
Для получения более крутых скатов АЧХ используют два или более согласованных Г-образных звеньев, соединяя их последовательно, чтобы образовать Т-образное звено (на Рис.3 сверху), или П-образное звено (на Рис.3 снизу). При этом получаются ФНЧ третьего порядка. Обычно, ввиду меньшего количества катушек, предпочитают П-образные звенья.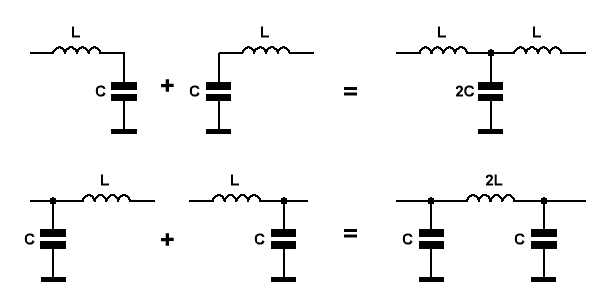

Рис.3 Последовательное соединение ФНЧ LC-фильтров

ФВЧ фильтры конструируют подобным же образом, лишь катушки заменяются конденсаторами, а конденсаторы - катушками. Полосовые LC - фильтры получают каскадным соединением ФНЧ и ФВЧ.

На самом деле, при проектировании многозвенных LC-фильтров высоких порядков, более грамотным решением (по сравнению с последовательным соединением фильтров низших порядков) будет их построение с использованием полиномов товарищей Чебышева, Баттерворта и других матёрых корифеев.
Именно такие фильтры 3-го, 5-го и 7-го порядков мы и рассмотрим на следующей странице.

Назад

Дальше