|
|||||||||||||||||||||||||||||||||||||||||||||||||
| Главная страница | Наши разработки | Полезные схемы | Это нужно знать | Вопросы-ответы | Весёлый перекур | |||||||||||||||||||||||||||||||||||||||||||||||||
| © 2017 Vpayaem.ru All Rights Reserved | |||||||||||||||||||||||||||||||||||||||||||||||||

|

|
Онлайн расчёт LC фильтров для акустики Калькулятор фильтров для акустических систем 1...6-го порядков: нижних частот (ФНЧ) для низкочастотных динамиков и сабвуферов,
фильтров верхних частот (ФВЧ) – для высокочастотных головок и полосовых фильтров (ПФ) – для среднечастотных. В настоящее время практически все качественные акустические системы являются многополосными, т. е. состоящими из нескольких
громкоговорителей, каждый из которых работает в своём, отведённом ему диапазоне частот. Для распределения энергии звукового сигнала
между динамиками используют электрические разделительные фильтры (КРОССОВЕРЫ), в данном рассматриваемом случае -
пассивные
LC-фильтры, которые включаются между выходным разъёмом усилителя, обладающего близким к нулю выходным сопротивлением, и
динамической головкой АС.
От себя добавлю, что действительно – фильтры 5-го порядка используются редко, однако если требуется существенное подавление внеполосных частот, подаваемых на сабвуфер, то в качестве ФНЧ, как правило, применяются фильтры не 5-го, а 6-го порядков и не Баттерворта, а Линквица – Райли. Приведём схемы LC фильтров верхних и нижних частот 6-го порядка. Схемы фильтров меньших порядков образуются путём отбрасывания соответствующих элементов (Рис.1). 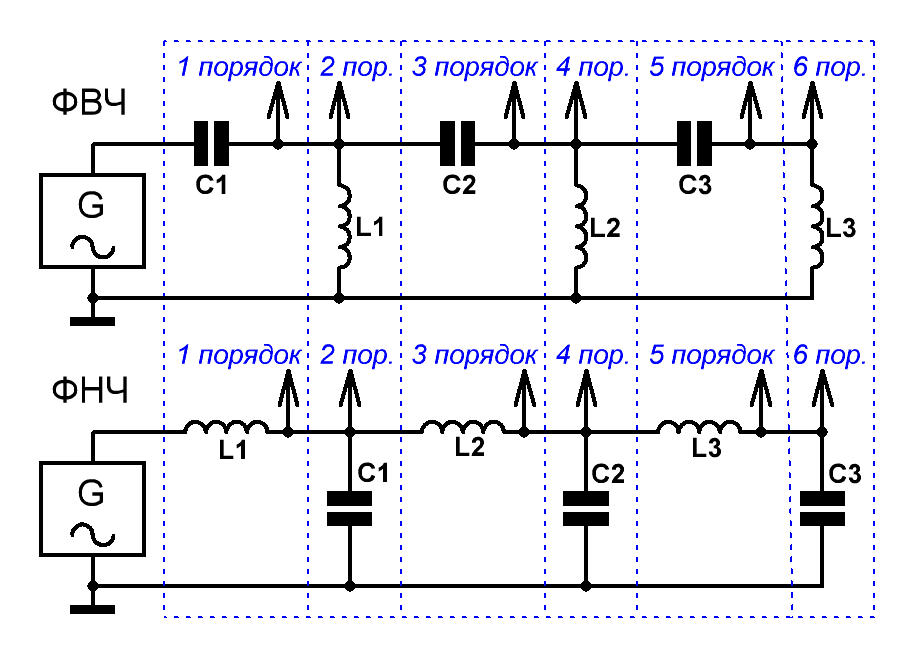 Рис.1 Схемы LC-фильтров верхних и нижних частот для акустики Для фильтров нижних частот – значения величин элементов, соответствующих: порядку фильтра, сопротивлению нагрузки Rн и частоте среза (разделения) Fср, рассчитываются по следующим формулам: Li= αi*Rн/(2πFср); Ci= αi/(2πFср*Rн), где αi – это справочные нормирован- ные значения (коэффициенты) для каждого элемента ФНЧ, называемые значениями элементов фильтра-прототипа. Для фильтров верхних частот – каждая индуктивность из схемы ФНЧ заменяется ёмкостью, ёмкость – индуктивностью, которые, исходя из тех же самых коэффициентов, рассчитываются по формулам: Ci= 1/(2πFср*αi*Rн) ; Li= Rн/(2πFср*αi) . Однако оставим все многочисленные таблицы со значениями нормированных коэффициентов фильтров-прототипов для справочной литературы, а сами сразу перейдём к онлайн расчёту номиналов элементов кроссоверов. Калькулятор расчёта ФНЧ и ФВЧ фильтров акустических систем При расчёте полосовых фильтров: каждый элемент-индуктивность из НЧ фильтра-прототипа заменяется на последовательный LC контур (Рис.2), элементы которого рассчитываются по следующим формулам: Li= αi*Rн/[2π(Fв - Fн)] , где Fн и Fв – нижняя и верхняя частоты среза поло- сового фильтра, а Ci= 1/(4π2*Fн*Fв*Li) . Каждый элемент-ёмкость из фильтра-прототипа нижних частот заменяется на параллельный LC контур, элементы которого рассчитываются по формулам: Ci= αi/[2π*Rн*(Fв - Fн)] ; Li= 1/(4π2*Fн*Fв*Ci). 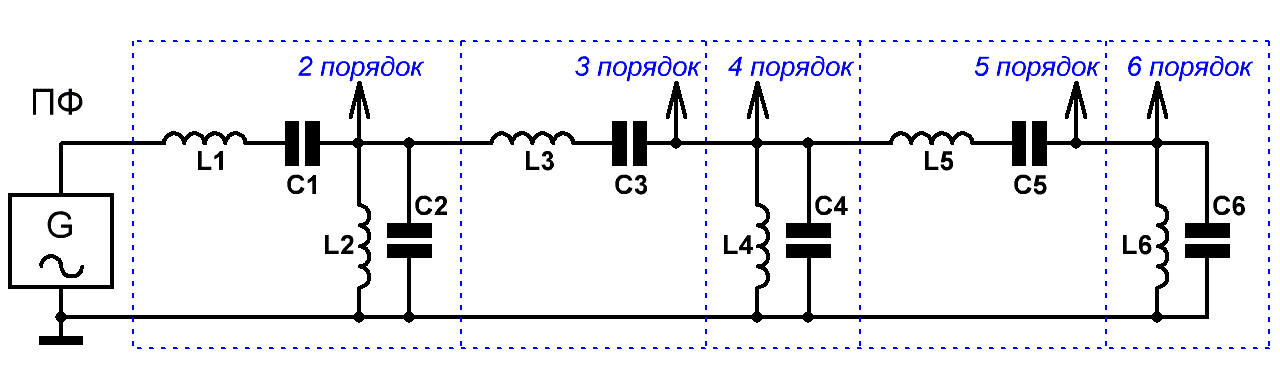 Рис.2 Схемы полосовых LC-фильтров для акустических систем Разместим калькулятор расчёта элементов и для этого типа фильтров: Калькулятор расчёта полосовых LC-фильтров для акустики При расчёте разделительных фильтров принимается допущение, что нагрузка (сопротивление динамика) – это величина чисто активная. Однако, учитывая то, что реальные громкоговорители обладают комплексным характером входного сопротивления, то для корректной работы фильтров могут потребоваться согласующие цепи, компенсирующие этот комплексный характер. При проектировании кроссоверов – частоты среза фильтров всегда следует выбирать значительно выше резонансных частот громкоговорителей. Тогда для компенсации комплексного характера входного сопротивления громкоговорителя будет достаточно включения упрощённой согласующей цепи, называемой цепью Цобеля и представляющей собой простую цепочку из последовательно включённых сопротивления Rк и ёмкости Cк (Рис.3а). Рэй Олден, автор одной из самых популярных книг по акустике, советует использовать следующие соотношения: Rк = 1,25*Rе ; Ск = Lе/Rе2, где Re и Le – это паспортные сопротивление и индуктивность динамика. 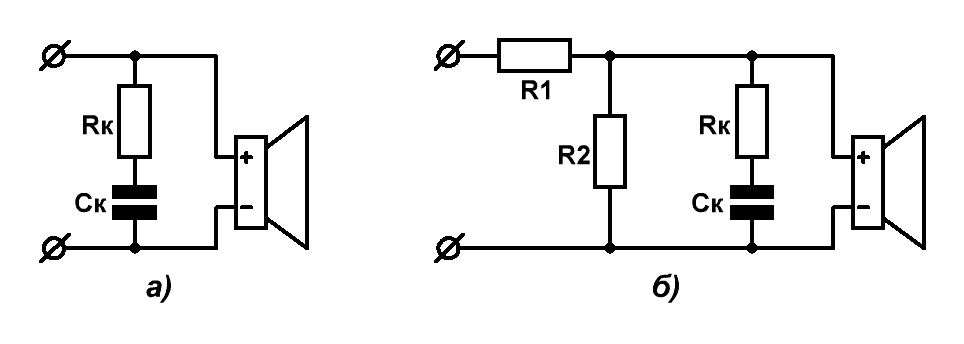 Рис.3 Цепь Цобеля и Г-образный аттенюатор для громкоговорителя Также для уменьшения неравномерности суммарной АЧХ многополосной АС зачастую необходимо ослабить уровень каких-либо составляющих, как правило – среднечастотных либо высокочастотных. Это можно сделать с помощью Г-образных пассивных аттенюаторов, обеспечивающих заданный уровень ослабления N (дБ) (Рис.3б). Если задаться целью произвести ослабление без коррекции активного сопротивления громкоговорителя, то формулы для вычисления номиналов резисторов имеют следующий вид: R1 ≈ Re*(100,05N - 1)/100,05N ; R2 ≈ Re/(100,05N - 1) . Сдобрим пройденный материал калькуляторами. Калькулятор расчёта цепи Цобеля для громкоговорителя Калькулятор расчёта аттенюатора для громкоговорителя Следует отметить, что некоторые производители акустики игнорируют согласующие цепи, считая, что компенсация комплексной характеристики портит звучание системы на реальном музыкальном материале. В таких случаях неравномерность АЧХ тракта приходится устранять при помощи измерительной аппаратуры, кропотливо подбирая каждый из элементов звеньев фильтра. В принципе – то же самое можно сделать и на симуляторе, подставив в качестве нагрузки фильтра эквивалентную электрическую схему громкоговорителя. Естественным образом – эта схема должна учитывать акустическое оформление динамика. А как создать такую схему, мы с вами подробно обсудили на странице – ссылка на страницу. | |||||||||||||||||||||||||||||||||||||||||